Vector review¶
Vectors: Physical quantities that have both direction and magnitude.
- Position, velocity, displacement, acceleration.
Represented as.
$$ \vec{R} ~or ~ \vec{R}_{B/A} ~ or ~ \vec{R}_{AB} $$Where A and B are tail and head of the vector.
Vectors with respect to coordinate frames.¶
Vectors can be representated with respect to a fixed or moving coordinate frame.
$$ \vec{a} = a_x \hat{i}+a_y \hat{j}+a_z \hat{k} = (a_x,a_y,a_z) $$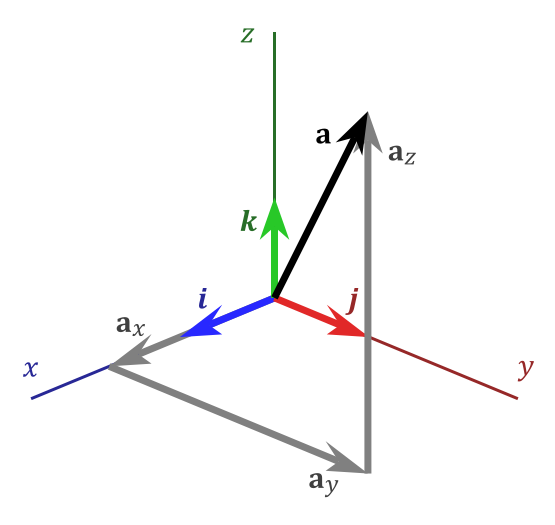
Taken from wikipedia.
Computing magnitude and direction¶
Given a vector, \( \vec{u} = u_x \hat{i}+u_y \hat{j}+u_z \hat{k} \)
The magnitude of vector is given by,
$$ |\vec{u}| = \sqrt{u_x^2+u_y^2+u_z^2} $$Directions are given via direction cosines,
$$ cos(\alpha) = \frac{u_x}{|\vec{u}|},cos(\beta) = \frac{u_y}{|\vec{u}|},cos(\gamma) = \frac{u_z}{|\vec{u}|}$$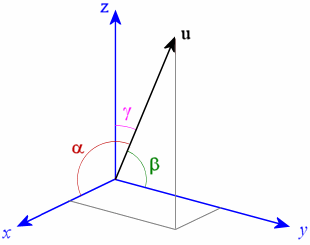
Magnitude and direction of a planar vector¶
Given, a vector \( \vec{u} = u_x \hat{i} + u_y \hat{j} \), the magnitude of the vector is given by,
$$ |\vec{u}| = \sqrt{u_x^2+u_y^2} $$The direction of the vector is given by,
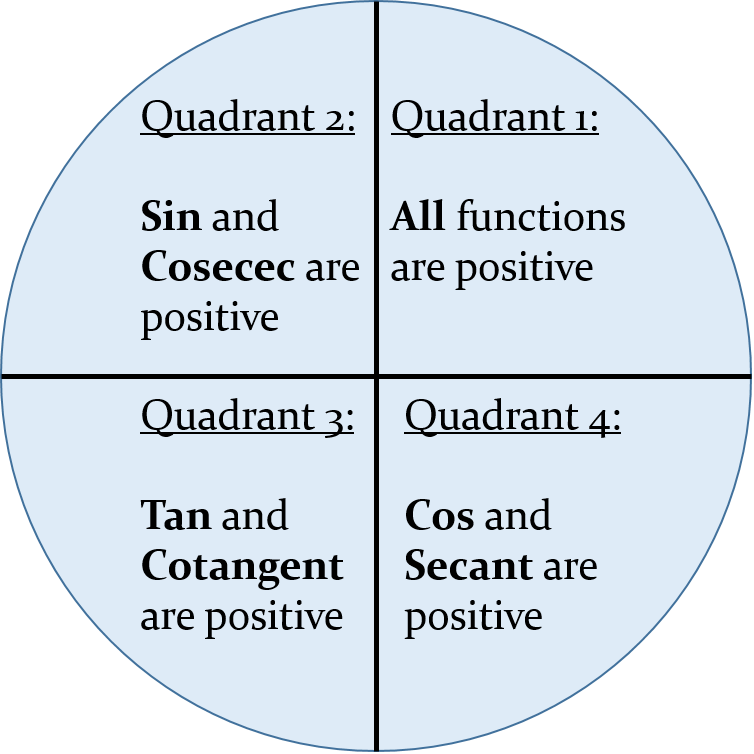
$$ \theta = atan2(u_y,u_x) $$Note, \( tan^{-1} \frac{u_y}{u_x} \) gives the angle, but needs to be corrected for the quadrant.
Sum of vectors¶
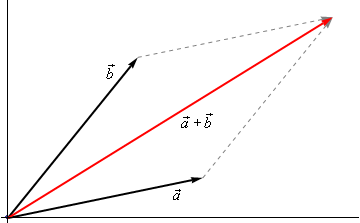
Sum of two vectors \( \vec{a} \) and \( \vec{b} \) is equal to the vector formed by the sum of their components.
Given two vectors
$$ \vec{a} = a_x \hat{i}+a_y \hat{j}+a_z \hat{k} $$$$ \vec{b} = b_x \hat{i}+b_y \hat{j}+b_z \hat{k} $$$$ \vec{a} + \vec{b} = (a_x + b_x) \hat{i}+ (a_y+b_y) \hat{j}+(a_z+b_z) \hat{k} $$Sum of vectors¶
Method 1:¶
Geometric method, to compute sum, move vectors so the tails of the vectors are aligned, and draw the diagonal of the parallelogram formed by the vectors.
Method 2:¶
- Move one vector so its tail coincides with the head of the other vector.
- Connect the tail of the first vector and head of the second vector or
Taken from, http://www.icoachmath.com/math_dictionary/addition_of_vectors.html
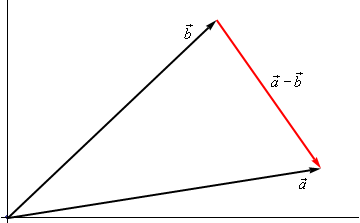
Difference of vectors¶
Difference of two vectors \( \vec{a} \) and \( \vec{b} \) is equal to the vector formed by the difference of their components.
Given two vectors
$$ \vec{a} = a_x \hat{i}+a_y \hat{j}+a_z \hat{k} $$$$ \vec{b} = b_x \hat{i}+b_y \hat{j}+b_z \hat{k} $$$$ \vec{a} - \vec{b} = (a_x - b_x) \hat{i}+ (a_y-b_y) \hat{j}+(a_z-b_z) \hat{k} $$Geometric method:¶
Geometric method, to compute different of two vectors, move vectors so the tails of the vectors are aligned, and connect head of the vector to be subtracted to the head of the other vector.
Dot product or Inner Product:¶
Dot product of two vectors \(\overrightarrow {a} \) and \( \overrightarrow {b} \) is defined as,
$$ \overrightarrow {a} \circ \overrightarrow {b} = \overrightarrow {a}^T \overrightarrow {b} = \sum_{i=1}^n a_i b_i $$where \(n\) is the length of the vectors \(\overrightarrow {a} \) and \( \overrightarrow {b}\).
For 3-D vectors,
$$ \overrightarrow {a} \circ \overrightarrow {b} = a_x b_x + a_y b_y + a_z b_z $$Interpretation of dot product¶
Dot product has several interpratations.
- Similarity measure: Inner product represents how similar two vectors are to one another. In the special case where, the vectors are normalized to have unit magnitude, then higher values indicates greater similarity between the vectors. This is also referred as Cosine similarity. $$ cos(\theta) = \frac{\overrightarrow {a} \circ \overrightarrow {b}}{ | \overrightarrow {a}| |\overrightarrow {b}|} ,$$
- Inner product also represents the length of the projection of one vector along the other vector. Therefore, the projection of vector (\overrightarrow {a}) along vector \(\overrightarrow {b}\) is $$ \frac{\overrightarrow {a} \circ \overrightarrow {b}}{ |\overrightarrow {b}|} .$$
Properties of dot product¶
- Dot products are scalars
- Dot product of two parallel vectors is equal to the product of the magnitudes of the vectors
- Dot product of two perpendicular vectors is equal to zero
- Dot product is commutative \( a \circ b = b \circ a \).
Cross product¶
- Cross product or vector product is defined between two vectors and is a measure of area of the parallelogram formed by the vectors.
\( \hat{u}_{a,b} \) is a unit vector perpendicular to both \( \vec{a} \) and \( \vec{b}\)
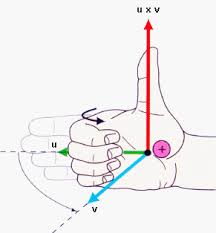
Right hand rule for cross product¶
- Align fingers along the first vector, while placing the base of the palm at the intersection of the two vectors.
- Curl fingers towards the second vector.
- The direction of cross product is given by the direction of the thumb.
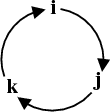
Cross product of unit vectors¶
Cross product of unit vectors can be obtained using the cycle below.
- Cross product of a vector by itself is zero.
- Cross product of a vector by another vector is equal to the third vector in the cycle, and the sign is determined by direction of rotation. If moving anti/counter-clockwise then positive, if clockwise then negative.
Direct computation of cross product.¶
Given two vectors
$$ \vec{a} = a_x \hat{i}+a_y \hat{j}+a_z \hat{k} $$$$ \vec{b} = b_x \hat{i}+b_y \hat{j}+b_z \hat{k} $$The cross product can be computed as,
$$ \vec{a} \times \vec{b} = (a_x \hat{i}+a_y \hat{j}+a_z \hat{k}) \times ( b_x \hat{i}+b_y \hat{j}+b_z \hat{k} ) $$$$ = a_x \hat{i} \times ( b_x \hat{i}+b_y \hat{j}+b_z \hat{k} ) + a_y \hat{i} \times ( b_x \hat{i}+b_y \hat{j}+b_z \hat{k} ) + a_z \hat{i} \times ( b_x \hat{i}+b_y \hat{j}+b_z \hat{k} ) $$Using formulas from previous slide for cross products of unit vectors,
$$ = (a_yb_z - a_z b_y) \hat{i} - (a_z b_x - a_x b_z) \hat{j} + (a_x b_y - a_y b_x) \hat{k} $$Cross product using matrix form¶
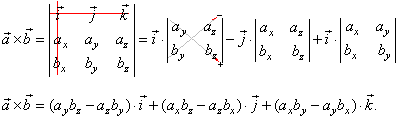
Properties of cross-product¶
- Cross products are VECTORS
- Cross product of two parallel vectors is equal to a null vector or zero.
- Cross product of two perpendicular vectors is equal to the magnitude of the vector, and the direction is given by right hand rule.
- Cross product is NOT commutative, infact \( a \times b = - b \times a \).