Overview¶
- Extending system of particles approach to rigid body
- Derive equations for 3D rigid body
- Planar rigid body
- Parallel axis theorm
Newton-Euler equation derivation for general rigid bodies¶
A rigid body can be considered as collection of infinite system of particles. For system of particles,
$$ \vec{F} = \left( \sum_{i=1}^N m_i \right) \vec{a}_G $$Applying equation above for infinite differential elements gives,
$$ \vec{F} = \left( \int_{body} d m \right) \vec{a}_G = M \vec{a}_G $$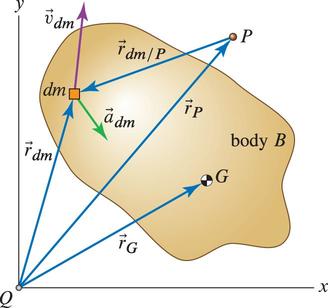
Angular momentum¶
Angular momentum of a rigid body about a point P can be written as,
$$ \vec{h}_p = \sum_{i=1}^N \vec{r}_{i/P} \times m_i \vec{v}_i $$For a rigid body,
$$ \vec{h}_p = \int_{body} \vec{r}_{dm/P} \times (dm) \vec{v}_{dm} = \int_{body} \vec{r}_{dm/P} \times \vec{v}_{dm} dm$$Taking derivative gives,
$$ \dot{\vec{h}}_p = \underbrace{ \int_{body} \vec{v}_{dm/P} \times \vec{v}_{dm} dm}_{I_1} + \underbrace{ \int_{body} \vec{r}_{dm/P} \times \vec{a}_{dm} dm}_{I_2} $$First integral
$$ I_1 = \int_{body} (\vec{v}_{dm} - \vec{v}_P) \times \vec{v}_{dm} dm = - \int_{body} \vec{v}_P \times \vec{v}_{dm} dm = - \vec{v}_P \times \int_{body} \vec{v}_{dm} dm $$$$ I_1 = - \vec{v}_P \times m \vec{v}_G $$Second integral
$$ I_2 = \int_{body} (\vec{r}_{dm/G} - \vec{r}_{P/G}) \times \vec{a}_{dm} dm = \int_{body} \vec{r}_{dm/G} \times \vec{a}_{dm} dm - \int_{body} \vec{r}_{P/G} \times \vec{a}_{dm} dm $$ $$ I_2 = \int_{body} \vec{r}_{dm/G} \times \vec{a}_{dm} dm - \vec{r}_{P/G} \times \int_{body} \vec{a}_{dm} dm = \int_{body} \vec{r}_{dm/G} \times \vec{a}_{dm} dm - \vec{r}_{P/G} \times m \vec{a}_G $$
$$ I_2 = \int_{body} \vec{r}_{dm/G} \times \vec{a}_{dm} dm - \vec{r}_{P/G} \times m \vec{a}_G = \int_{body} \vec{r}_{dm/G} \times \vec{a}_{dm} dm + \vec{r}_{G/P} \times m \vec{a}_G $$
$$ I_2 = \int_{body} \vec{r}_{dm/G} \times [\vec{a}_{G} + \vec{\alpha}_B \times \vec{r}_{dm/G} + \vec{\omega}_B \times ( \vec{\omega}_B \times\vec{r}_{dm/G}) ] dm + \vec{r}_{G/P} \times m \vec{a}_G $$
$$ I_2 = \underbrace{ \int_{body} \vec{r}_{dm/G} \times \vec{a}_{G} dm }_{=0} + \int_{body} \vec{r}_{dm/G} \times ( \vec{\alpha}_B \times \vec{r}_{dm/G} ) dm + \int_{body} \vec{r}_{dm/G} \times (\vec{\omega}_B \times ( \vec{\omega}_B \times\vec{r}_{dm/G})) dm + \vec{r}_{G/P} \times m \vec{a}_G $$
$$ I_2 = \int_{body} \vec{r}_{dm/G} \times ( \vec{\alpha}_B \times \vec{r}_{dm/G} ) dm + \int_{body} \vec{r}_{dm/G} \times ( \vec{\omega}_B \times ( \vec{\omega}_B \times\vec{r}_{dm/G}) ) dm + \vec{r}_{G/P} \times m \vec{a}_G $$
Using vector triple product, \( \vec{a} \times ( \vec{b} \times \vec{c} ) =\vec{b} ( \vec{a} \circ \vec{c} ) - \vec{c} ( \vec{a} \circ \vec{b} ) \)¶
$$ I_2 = \int_{body} \vec{r}_{dm/G} \times ( \vec{\alpha}_B \times \vec{r}_{dm/G} ) dm + \int_{body} \vec{r}_{dm/G} \times ( \vec{\omega}_B \times ( \vec{\omega}_B \times \vec{r}_{dm/G}) ) dm + \vec{r}_{G/P} \times m \vec{a}_G $$ $$ I_2 = \int_{body} [\vec{\alpha}_B ( \vec{r}_{dm/G} \circ \vec{r}_{dm/G}) - \vec{r}_{dm/G} ( \vec{r}_{dm/G} \circ \vec{\alpha}_B )] dm $$$$ + \int_{body} \vec{r}_{dm/G} \times ([ \vec{\omega}_B ( \vec{r}_{dm/G} \circ \vec{\omega}_B ) - \vec{r}_{dm/G} ( \vec{\omega}_B \circ \vec{\omega}_B )] ) dm $$$$ + \vec{r}_{G/P} \times m \vec{a}_G $$
$$ I_2 = \int_{body} [\vec{\alpha}_B ( \vec{r}_{dm/G} \circ \vec{r}_{dm/G}) - \vec{r}_{dm/G} ( \vec{r}_{dm/G} \circ \vec{\alpha}_B )] dm $$$$ + \int_{body} \vec{r}_{dm/G} \times \vec{\omega}_B ( \vec{r}_{dm/G} \circ \vec{\omega}_B ) dm $$$$ + \vec{r}_{G/P} \times m \vec{a}_G $$
Planar rigid body¶
For planar case, all motion is along the axis perpendicular to body, therefore, \( \vec{r} \times \vec{\alpha} = 0 \) and \( \vec{r} \times \vec{\omega} = 0 \)
$$ I_2 = \int_{body} [\vec{\alpha}_B ( \vec{r}_{dm/G} \circ \vec{r}_{dm/G}) - \vec{r}_{dm/G} ( \vec{r}_{dm/G} \circ \vec{\alpha}_B )] dm $$$$ + \int_{body} \vec{r}_{dm/G} \times \vec{\omega}_B ( \vec{r}_{dm/G} \circ \vec{\omega}_B ) dm $$$$ + \vec{r}_{G/P} \times m \vec{a}_G $$
$$ I_2 = \int_{body} \vec{\alpha}_B ( \vec{r}_{dm/G} \circ \vec{r}_{dm/G}) dm + \vec{r}_{G/P} \times m \vec{a}_G $$ $$ I_2 = \int_{body} |\vec{r}_{dm/G}|^2 dm \vec{\alpha}_B + \vec{r}_{G/P} \times m \vec{a}_G $$Substituting gives¶
$$ \dot{\vec{h}}_p = \underbrace{ \int_{body} \vec{v}_{dm/P} \times \vec{v}_{dm} dm}_{I_1} + \underbrace{ \int_{body} \vec{r}_{dm/P} \times \vec{a}_{dm} dm}_{I_2} $$ $$ \dot{\vec{h}}_p = - \vec{v}_P \times m \vec{v}_G + \int_{body} |\vec{r}_{dm/G}|^2 dm \vec{\alpha}_B + \vec{r}_{G/P} \times m \vec{a}_G $$ $$ \dot{\vec{h}}_p + \vec{v}_P \times m \vec{v}_G = \int_{body} |\vec{r}_{dm/G}|^2 dm \vec{\alpha}_B + \vec{r}_{G/P} \times m \vec{a}_G $$Recall,
$$ \vec{M}_P = \dot{\vec{h}}_p + \vec{v}_P \times m \vec{v}_G $$Final equation¶
Force equation,
$$ \vec{F} = m \vec{a}_G $$Torque equation,
$$ \vec{M}_P = \dot{\vec{h}}_p + \vec{v}_P \times m \vec{v}_G = \int_{body} |\vec{r}_{dm/G}|^2 dm \vec{\alpha}_B + \vec{r}_{G/P} \times m \vec{a}_G $$ $$ \vec{M}_P = I_G \vec{\alpha}_B + \vec{r}_{G/P} \times m \vec{a}_G $$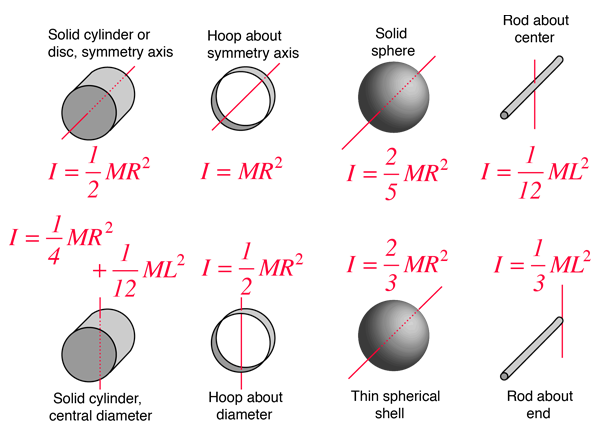
Parallel axis theorem¶
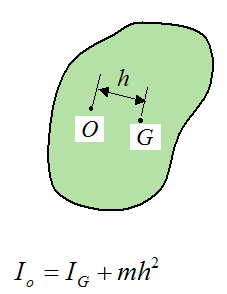
EXAMPLE¶
In [ ]: