Rigid body¶
A body is considered rigid body if it cannot be deformed. Rigid body has following properties,
- Distance between any 2 points on the body is constant under any transformation.
- 3 points on the body completely define the pose of the body (this is true for 3D and 2D).
- Angular velocity of all points on the body is the same (this is true for 3D and 2D), therefore angular momentum is propery of the
Planar motions are motions that occur in a plane.¶
Planar rigid body motions are motions of rigid body that occur in a plane.¶
Two types of planar motions¶
- Translation: Moving so the pose of the body does not change
- Rotation: Rotation motion about a fixed axis.
General motion of rigid body can be expressed as combination of rotation and translation.
Velocity¶
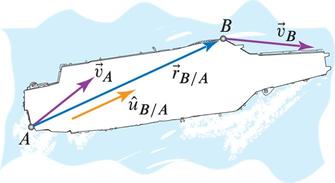
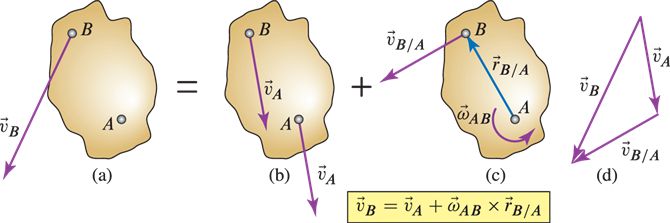
$$ \vec{v}_{B} = \vec{v}_{A} + \vec{v}_{B/A} $$As the body is rigid,
- \( | \vec{r}_{B/A} | \) is constant, and
- \( \vec{v}_{B/A} \) can only execute a rotational motion about \( A \),
Recall, general velocity is \( \vec{v} = \dot{r} \hat{u}_r + \vec{ \omega} \times \vec{r } \)
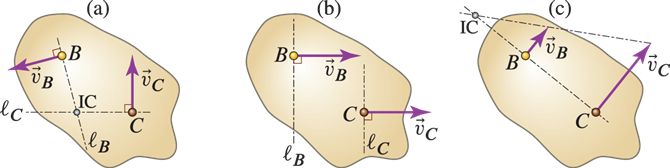
VELOCITY EXAMPLE¶
Acceleration¶
$$ \vec{a}_{B} = \vec{a}_{A} + \vec{a}_{B/A} $$As the body is rigid,
- \( | \vec{r}_{B/A} | \) is constant, and
- \( \vec{a}_{B/A} \) can only execute a rotational motion about \( A \)
Recall, general acceleration is \( \vec{a} = \ddot{r} \hat{u}_r + \vec{\alpha} \times \vec{r } + 2 \dot{r} \vec{\omega} \times \hat{u }_r + \vec{\omega} \times (\vec{\omega} \times \vec{r})\)
Planar Acceleration¶
In special case when direction of rotation is perpendicular to the plane of motion, and all rotation is about only 1 axis,
$$ \vec{a}_{B} = \vec{a}_{A} +\vec{\alpha}_{AB} \times \vec{r}_{B/A} + \vec{\omega}_{AB} \times (\vec{\omega}_{AB} \times \vec{r}_{B/A} ) $$becomes
$$ \vec{a}_{B} = \vec{a}_{A} +\vec{\alpha}_{AB} \times \vec{r}_{B/A} - |\vec{\omega}_{AB}|^2 \vec{r}_{B/A} $$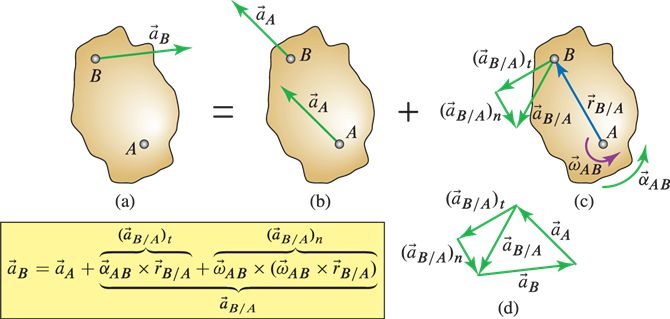
Example¶
Rotating-frame¶
$$ \vec{r}_p = \vec{r}_A + \vec{r}_{P/A} $$$$ = \vec{r}_A + \vec{\rho} $$$$ = \vec{r}_A + \rho \hat{u}_{\rho} $$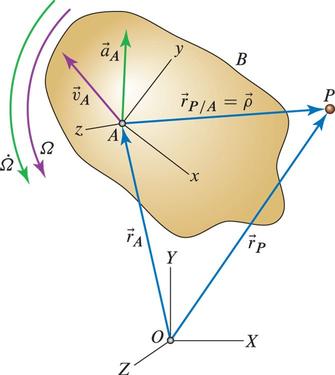
Using calculus of vectors,¶
$$ \vec{r}_P = \vec{r}_A + \rho \hat{u}_{\rho} $$$$ \vec{v}_P = \vec{v}_A + \dot{\rho} \hat{u}_{\rho} +\vec{\Omega} \times \vec{\rho} $$$$ \vec{a}_P = \vec{a}_A + \ddot{\rho} \hat{u}_{\rho} +2 \dot{\rho} \vec{\Omega} \times \hat{u}_\rho + \dot{\vec{\Omega}} \times \vec{\rho} + \vec{\Omega} \times (\vec{\Omega} \times \vec{r}) $$$$ \vec{a}_P = \vec{a}_A + \ddot{\rho}_{rel} +2 \vec{\Omega} \times \dot{\vec{\rho}}_{rel} + \dot{\vec{\Omega}} \times \vec{\rho} + \vec{\Omega} \times (\vec{\Omega} \times \vec{r}) $$EXAMPLE 1¶
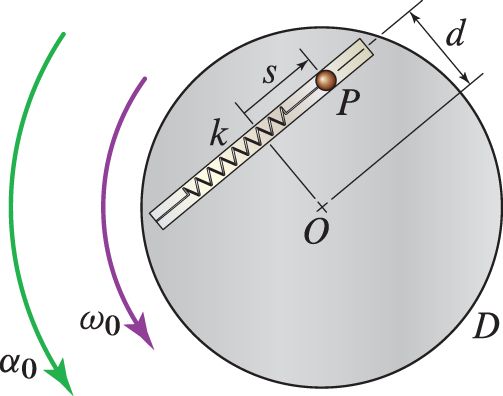
EXAMPLE 2¶
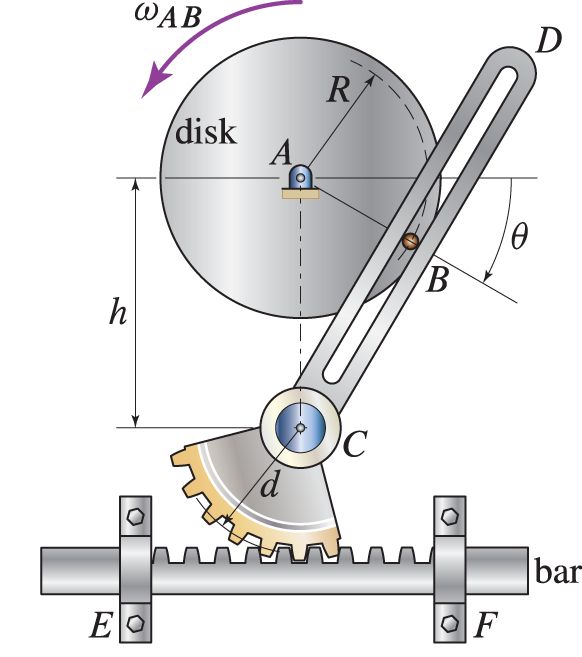
In [ ]: