Angular momentum¶
Given a particle at Q, the angular momentum about a point P is given by,
$$ \vec{h}_{P} = \vec{r}_{Q/P} \times \vec{p}_Q = \vec{r}_{Q/P} \times m \vec{v}_Q $$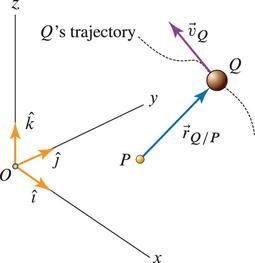
Angular momentum-impulse principle¶
Taking derivative of angular momentum gives
$$ \dot{\vec{h}}_p = \frac{d (\vec{r}_{Q/P} \times m \vec{v}_Q)}{dt} $$ $$ \dot{\vec{h}}_p = \vec{v}_{Q/P} \times m \vec{v}_Q+ \vec{r}_{Q/P} \times m \vec{a}_Q $$As \( \vec{v}_{Q/P} = \vec{v}_Q - \vec{v}_P \),
$$ \dot{\vec{h}}_p = (\vec{v}_{Q} - \vec{v}_{P}) \times m \vec{v}_Q+ \vec{r}_{Q/P} \times m \vec{a}_Q $$As Net force \( F = m \vec{a}_Q \),
$$ \dot{\vec{h}}_p = - \vec{v}_{P} \times m \vec{v}_Q+ \vec{r}_{Q/P} \times \vec{F}_Q $$Rearranging gives,
$$ \vec{r}_{Q/P} \times \vec{F}_Q = \dot{\vec{h}}_p + \vec{v}_{P} \times m \vec{v}_Q $$We define moment \( \vec{M} \) as,
$$ \vec{M}_Q = \vec{r}_{Q/P} \times \vec{F}_Q $$to get,
$$ \vec{M}_Q = \dot{\vec{h}}_p + \vec{v}_{P} \times m \vec{v}_Q $$In special case when¶
- \( \vec{v}_P = 0 \) or
- \( \vec{v}_{P} \times \vec{v}_Q = 0 \)
Integrating gives,
$$ \vec{h}_{p,2} - \vec{h}_{p,1} = \int_{t_1}^{t_2} \vec{M}_Q dt $$if net moment at \( Q \) is equal to zero, angular momentum is conserved
$$ \vec{h}_{p,2} = \vec{h}_{p,1} $$EXAMPLE¶
Angular momentum for system of particles¶
For each particle \( i \) we have,
$$ \vec{M}_{i} = \dot{\vec{h}}_{P,i} + \vec{v}_{P} \times m_i \vec{v}_{i} $$|
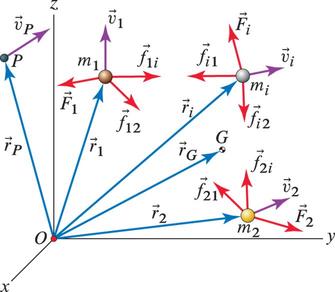
The first term is,
$$ \vec{M}_{i} = \vec{r}_{i/P} \times (\vec{F_i} + \vec{f}_{ij} ) $$Newton's third law states that every action has equal and opposite reaction, therefore,
$$ \vec{f}_{ij} = - \vec{f}_{ji} $$and
$$ \vec{r}_{i/P} \times \vec{f}_{ij} = - \vec{r}_{j/P} \times \vec{f}_{ji} $$Therefore, adding over all particles cancels out the contribution of internal moments.
As adding over all particles cancels out contribution of internal moments,
$$ \sum_{i} \vec{M}_{i} = \sum_{i} \vec{r}_{i/P} \times \vec{F_i} $$Adding the right hand side terms,
$$ \sum_{i} \dot{\vec{h}}_{P,i} + \sum_{i} \vec{v}_{P} \times m_i \vec{v}_{i} $$ $$ = \dot{\vec{h}}_{P} + \vec{v}_{P} \times m \vec{v}_{G} $$Therefore for multiple particles,
$$ \sum_{i} \vec{r}_{i/P} \times \vec{F_i} = \dot{\vec{h}}_{P} + \vec{v}_{P} \times m \vec{v}_{G} $$In special case when¶
- \( \vec{v}_P = 0 \) or
- \( \vec{v}_{P} \times \vec{v}_G = 0 \)
In [ ]: