Momentum-impulse principle¶
Momentum-impulse principle states that,
$$ \vec{F} = \dot{\vec{p}} $$where \( \vec{p} = m \vec{v} \) is called momentum of the particle.
Momentum and impulse¶
$$ \vec{F} = m \vec{a} = m \frac{d \vec{v}}{ dt} $$Integrating gives,
$$ \underbrace{\int_{t_1}^{t_2} \vec{F} dt}_{Impulse} = m \vec{v}_2 - m \vec{v}_1 $$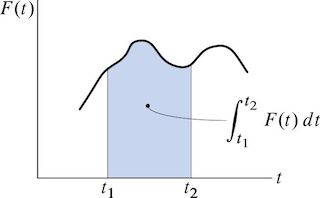
Impulse¶
$$ Impulse = \int_{t_1}^{t_2} \vec{F} dt $$$$ Average ~force = \frac{\int_{t_1}^{t_2} \vec{F} dt }{t_2 - t_1}$$
Momentum and impulse for a system of particles¶
$$ \vec{F}_i + \sum_{N,i \neq j} \vec{f}_{ij}= \dot{\vec{p}}_i $$Adding for all particles gives,
$$ \sum_{N} \vec{F}_i + \sum_{N} \sum_{N,i \neq j}\vec{f}_{ij}= \sum_{N} \dot{\vec{p}}_i $$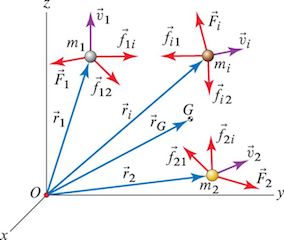
$$ \sum_{N} \vec{F}_i = \sum_{N} m_i \vec{v}_i = m_T \vec{v}_G $$$$ \vec{v}_G = \frac{ \sum_N m_i \vec{v}_i}{\sum_N m_i } $$
Conservation of linear momentum¶
If the net external force on a particle is zero, the momentum is conserved.
$$ \underbrace{\int_{t_1}^{t_2} \vec{F} dt}_{Impulse} = \sum_N \vec{p}_2 - \sum_N \vec{p}_1 $$If net external force is zero,
$$ \sum_N \vec{p}_2 = \sum_N \vec{p}_1 $$Impact¶
When multiple bodies undergo idealized impact, the component of velocity perpendicular to the line of impact does not change, and the component of velocity along the line of impact changes according to momentum conservation principle.

Central impact¶
Momentum before impact,
$$ m_A v_A^- + m_B v_B^- $$Momentum after impact,
$$ m_A v_A^+ + m_B v_B^+ $$Momentum conservation states,
$$m_A v_A^- + m_B v_B^- = m_A v_A^+ + m_B v_B^+ $$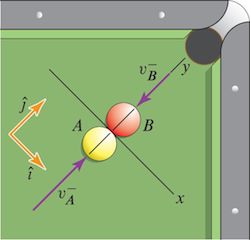
Coefficient of restitution¶
$$ e = \frac{v_B^+ - v_A^+ }{v_A^- - v_B^- } $$An impact is said to be
- plastic if \(e = 0\),
- elastic if \( 0 < e < 1 \)
- perfectly elastic if \(e = 1 \)
In [ ]: