Energy methods for particles

Vivek Yadav, PhD

MEC 262: Engineering Dynamics (4.1 to 4.4)

Recap: Why use energy methods

1. Newton's force laws,
   • vector based
   • prone to error
   • Need to perform complex integration
2. Energy methods,
   • scalar relations,
   • less prone to error,
   • Write relations only at start and end positions

Energy methods are compact and less prone to errors.

Work-energy principle

$$ \underbrace{\int_{L_{1-2}} \vec{F} \circ d \vec{r}}_{work} = \underbrace{\frac{1}{2}m (v_2^2 - v_1^2)}_{Change~ in~ Kinetic~ Energy}$$$$ U_{1-2} = T_2 - T_1 $$

where,

• \( U_{1-2}\) is the work done by the force to move particle from 1 to 2.
• \( T_i\) is the kinetic energy at instant \( i \).

Work done by a force

$$ U_{1-2} = \int_1^2 \vec{F} \circ d\vec{s} $$

Energy law:

Work done by external forces is equal to the change in kinetic energy

$$ U_{1-2} + T_1 = T_2$$

Work energy principle for a system of particles

Forces for a system of particles,

$$ \vec{F}_i + \vec{f}_{ij} = m_i \vec{a}_i $$

Work done by forces

$$ \int_{L_{1-2}} \sum_{i=1}^N (\vec{F}_i + \vec{f}_{ij}) \circ d\vec{r} $$

$$ \int_{L_{1-2}} \sum_{i=1}^N \vec{F}_i \circ d\vec{r} + \int_{L_{1-2}} \sum_{i=1}^N \vec{f}_{ij} \circ d\vec{r} $$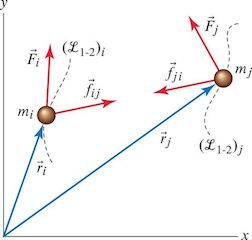

$$ \int_{L_{1-2}} \sum_{i=1}^N \vec{F}_i \circ d\vec{r} + \int_{L_{1-2}} \sum_{i=1}^N \vec{f}_{ij} \circ d\vec{r_{i/j}} $$

$$ \underbrace{\int_{L_{1-2}} \sum_{i=1}^N \vec{F}_i \circ d\vec{r} }_{external ~ work} + \underbrace{\int_{L_{1-2}} \sum_{i=1}^N \vec{f}_{ij} \circ d\vec{r_{i/j}}}_{internal ~ work} $$

Further splitting forces into conservative and non-conservative, and using,

$$ U_{c,1-2} = -(V_2-V_1), $$

Work done by the external and internal forces becomes,

$$ U_{nc,1-2} + U_{int,1-2} - (V_2 - V_1)$$

As work done by all the forces is equal to change in kinetic energy,

$$ U_{nc,1-2} + U_{int,1-2} - (V_1 - V_2) = T_2-T_1$$

Rearranging gives,

$$ U_{nc,1-2} + U_{int,1-2} + T_1 + V_1 = T_2+V_2$$

Kinetic energy of system of particles

$$ T = \frac{1}{2} m_i v_i^T \circ v_i $$

Write velocity as,

$$ T = \frac{1}{2}\sum_{i=1}^N m_i (v_G + v_{i/G})^T \circ (v_G + v_{i/G}) $$

$$ T = \frac{1}{2}\sum_{i=1}^N m_i (v_G \circ v_G + 2 v_G \circ v_{i/G} + v_{i/G}^T v_{i/G}) $$

$$ T = \frac{1}{2}\sum_{i=1}^N m_i v_G \circ v_G + \underbrace{2 \frac{1}{2}\sum_{i=1}^N m_i v_G \circ v_{i/G}}_{=0} + \frac{1}{2}\sum_{i=1}^N m_i v_{i/G}^T v_{i/G}) $$

$$ T = \frac{1}{2} m v_G \circ v_G + \frac{1}{2}\sum_{i=1}^N m_i v_{i/G}^T v_{i/G}) $$

Dividing forces as conservative and nonconservative forces,

Work done by external forces is equal to the change in kinetic energy

$$ U_{nc,1-2} + U_{int,1-2} + T_1 + V_1= T_2 + V_2 $$

where

• \( U_{nc,1-2} \) is the work done by non-conservative forces.
• \( U_{in,1-2} \) is the work done by internal forces.
• And kinetic energy is given by, $$ T = \frac{1}{2} m v_G \circ v_G + \frac{1}{2}\sum_{i=1}^N m_i v_{i/G}^T v_{i/G}) $$

Recall

Conservative forces

Conservative forces are forces where the work done between two points depends solely on the initial and final positions of the particle. Example, gravity, spring, etc.

Non-conservative forces

Non-conservative forces are forces where the work done between two points depends solely on the PATH taken between the initial and final positions of the particle. Example, movement under friction or viscous fields.

Work done by tension

Work done by an inextensible cord in a pulley system is equal to 0.

EXAMPLE

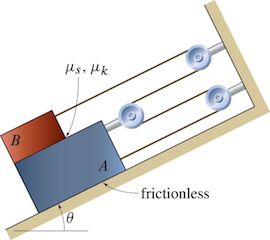
Friction example of work done by internal force

The two blocks A and B of mass \( m_A = 4 \) kg and \( m_B = 1 \) kg, respectively, are connected by an inextensible cord and the pulley system shown. There is negligible friction between A and the θ = 30° incline, and the coefficient of kinetic friction between A and B is \( \mu_k = 0.1 \). Assuming that \( \mu_s \) is insufficient to prevent slipping and that the system is released from rest, determine the velocity of A and B after B has moved up the incline a distance \( d = 0.35 \) m relative to A.