Relation to Newton's law (\( \vec{F} = m \vec{a} \)).¶
From Newton's second law,
$$ \vec{F} = m \vec{a} $$Taking dot product with the displacement vector gives,
$$ \vec{F} \circ d \vec{r} = m \vec{a} \circ d \vec{r} $$As \( d \vec{r} = \vec{v} dt \) and \( \vec{a} = d \vec{v}/dt \),
$$ \vec{F} \circ d \vec{r} = m \vec{a} \circ d \vec{r} = m \vec{v} \circ d \vec{v} $$Integrating and assuming no mass change gives,
$$ \int_{L_{1-2}} \vec{F} \circ d \vec{r} = \int_{v_1}^{v_2} m \vec{v} \circ d \vec{v} $$$$ \int_{L_{1-2}} \vec{F} \circ d \vec{r} = \frac{1}{2}m (v_2^2 - v_1^2)$$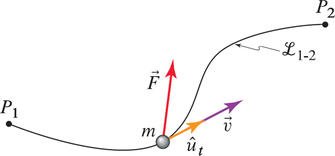
Work-energy principle¶
$$ \underbrace{\int_{L_{1-2}} \vec{F} \circ d \vec{r}}_{work} = \underbrace{\frac{1}{2}m (v_2^2 - v_1^2)}_{Change~ in~ Kinetic~ Energy}$$$$ U_{1-2} = T_2 - T_1 $$where,
- \( U_{1-2}\) is the work done by the force to move particle from 1 to 2.
- \( T_i\) is the kinetic energy at instant \( i \).
Work done by the forces acting on a particle is equal to change in kinetic energy. Units of work are Joules (J), and in some cases is also expressed as (N-m).
Work done by forces perpendicular to direction of motion is zero, eg. Normal reaction when particle is moving horizontally.
Steps for solving Work-energy problems¶
- Identify initial and final positions of interest.
- Draw Free body diagram
- Compute work done by all the forces on the body.
- Equate work done to change in Kinetic energy.
Conservative forces¶
A conservative force is a force with the property that the work done in moving a particle between two points is independent of the taken path.
<img src = 'images/Conservative.png'>
Work done by the constant force of gravity¶
Force due to gravity is \( \vec{F} = - mg \hat{j} \), work done by gravity in moving particle from 1 to 2 is,
$$ U_{1-2} = \int_1^2 \vec{F} \circ d\vec{s} = \int_1^2 (-mg \hat{j}) \circ (dx \hat{i} + dy \hat{j}) $$$$ U_{1-2} = -mg \int_1^2 dy = -mg(y_2-y_1) $$<img src = 'images/gravity_work.jpg'>
Work done by the constant force of gravity¶
Using \( U_{1-2} = T_2 - T_1 \),
$$ -mg(y_2-y_1) = T_2 - T_1 $$$$ -mgy_2+mgy_1 = T_2 - T_1 $$Rearranging gives,
$$ T_1 + mgy_1 = T_2 + mgy_2 $$Work done by spring force¶
$$ U_{1-2} = \int_1^2 \vec{F} \circ d \vec{r} = \int_1^2 -kx dx$$ $$ U_{1-2} = -k \int_1^2 x dx = -\frac{1}{2}k(x_2^2 - x_1^2) $$Using in \( U_{1-2} = T_2 - T_1 \) gives,¶
$$ -\frac{1}{2}k(x_2^2 - x_1^2) = T_2 - T_1 $$Rearranging gives,
$$ T_1 + \frac{1}{2}kx_1^2 = T_2 + \frac{1}{2}kx_2^2 $$Potential fields and potential energy¶
In cases where the work done by a particle depends only on the initial and final position, and not the path taken, the ability to do work at different regions of space can be expressed via a potential function \( V \).
We define \( V \) so that,
$$ - \vec{\nabla} V = \vec{F} $$where \( \nabla \) is the gradient operator.
Work done can be expressed as,
$$ U_{1-2} = \int_1^2 \vec{F} \circ d \vec{r} = - \int_1^2 \vec{\nabla} V = -(V_2 - V_1) $$Using in \( U_{1-2} = T_2 - T_1 \) gives,¶
$$ -(V_2 - V_1) = T_2 - T_1 $$$$ V_2 +T_2 = V_1 + T_1 $$Potential Energy:
gravitational force is mgy (y is measured w.r.t a datum)
Spring force is \( \frac{1}{2} k x^2 \).
EXAMPLE¶