Overview¶
- Applying Newton's law for particle motion
- Express Newton's laws in Rectilinear, Normal-Tangent (path) coordinates and Polar coordinates
- As particles are represented by a mass concentrated at a point, the forces must be concurrent, i.e. pass through the same point.
Applying Newton's Laws of motion¶
$$ \vec{F} = m \vec{a} $$Steps to applying newton's laws
- Set up coordinate system and draw free body diagram
- Draw all the forces acting on the particle
- Express forces along the axes of coordinate systems
- Add forces along individual axes, and equate to the mass of the particle times the acceleration along the axes.
- Solve for unknown values
- Perform sanity checks to verify if the solutions make physical sense.
Force laws¶
- Friction
- Tension
- Spring force
- Gravity
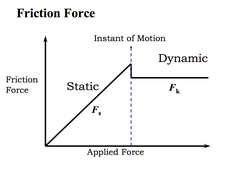
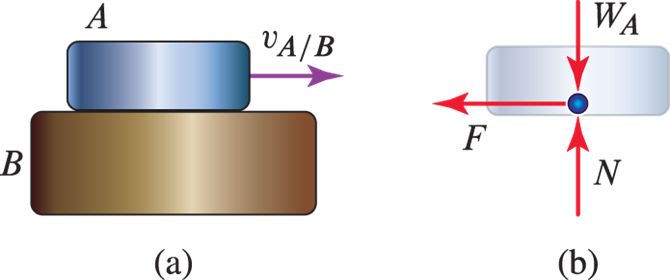
1. Friction¶
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. Note, friction always opposes the tendency of motion.
- Static friction \( F \leq \mu_s N \) when there is no motion between the particle and surface
- Dynamic friction \( F = \mu_k N \), when there is motion between the surfaces
Friction force
- Static friction \( F \leq \mu_s N \) when there is no motion between the particle and surface
- Dynamic friction \( F = \mu_k N \), when there is motion between the surfaces
2. Tension¶
The tension force is the force that is transmitted through a string, rope. The tension force is directed along the length of the wire and pulls equally on the objects on the opposite ends of the wire.
- Tension force cannot be negative
- Tension acting via rope or cable can only apply pulling force, not pushing force.
- Tension is the same at all points in a cable, assuming massless cable and frictionless pulleys
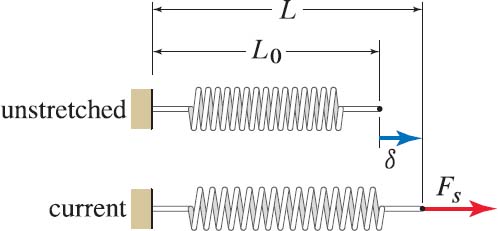
3. Spring force¶
Force of a spring is given by
$$ F_s = - K(L-L_0) $$where, \( K \) is the stiffness of the spring, \( L \) is spring's length and \( L_0 \) is the slack length.
3.2 Cuvilinear motion¶
- Cartesian coordinate frame
- Normal-tangential (path) coordinate systems
- Polar coordinate systems
1. Cartesian coordinate frame¶
$$ \sum F_x = m a_x = m \ddot{x}$$ $$ \sum F_y = m a_y = m \ddot{y} $$
2. Normal-tangential (path) coordinate systems¶
$$ \sum F_t = m a_t = m \dot{v}$$ $$ \sum F_n = m a_n = m \frac{v^2}{\rho} $$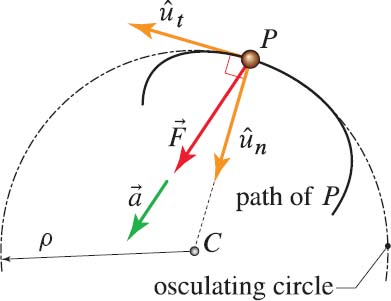
Axis for Normal-tangential system¶
- \( \hat{u}_t \) is along the direction of velocity of the particle
- \( \hat{u}_n \) is pointed towards the center of the osculating circle.
3. Polar coordinate systems¶
$$ \sum F_r = m a_r = m ( \ddot{r} - r \omega^2)$$ $$ \sum F_\theta = m a_\theta = m ( r \ddot{\theta} + 2 \dot{r} \dot{\theta}) $$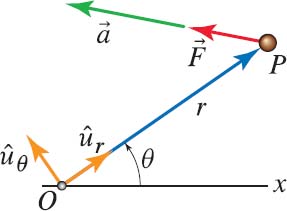
Axis for Polar system¶
- \( \hat{u}_r \) is pointed from origin to the particle's location.
- \( \hat{k} \) is pointed along the direction of positive angle
- \( \hat{u}_\theta \) is computed as cross product of \( \hat{k} \) and \( \hat{u}_r \)
If the above conditions hold,
$$ \vec{a} = ( \ddot{r} - \omega^2 r) \hat{u}_r + ( r \ddot{\theta} - 2 \dot{ \omega} \dot{r}) \hat{u}_\theta $$System of particles¶
Derive equations of motion for multiple particles under action of an external force and internal forces.
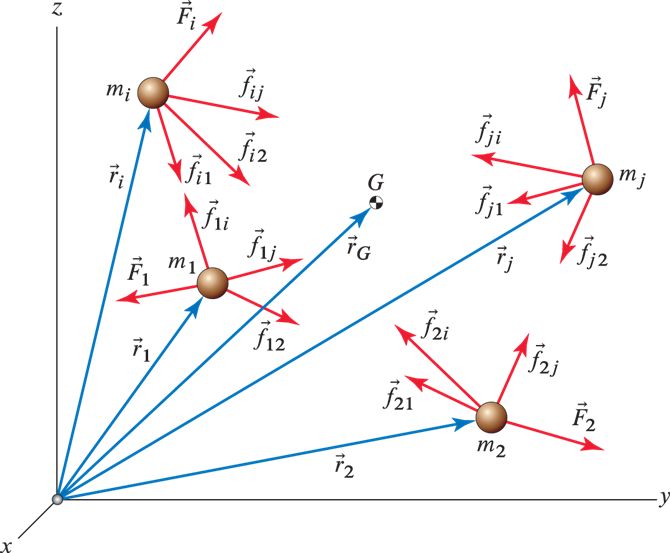
Assumptions:
- Internal forces act between the particles
- External forces are acted upon the particles by an external force
- \( \vec{F}_{ij} \) represents force of particle \(j\) acting on \(i\).
Newton law for system of particles¶
$$ \sum F_i = m_i \vec{a}_i $$ $$ F_i + \sum_{i \neq j} F_{ij} = m_i \vec{a}_i $$Adding for all particles gives,
$$ \sum_{particles}F + \sum_{particles} \sum_{i \neq j} F_{ij} = \sum_{particles}m_i \vec{a}_i $$As internal forces are equal and opposite, they add up to zero.
$$ \sum_{particles}F = \sum_{particles}m_i \vec{a}_i $$Define a point called center of mass such that,
$$ \sum_{particles}F = \sum_{particles}m_i \vec{a}_i = \left(\sum m_i \right) \vec{a}_{cm}$$Rewriting above equation gives,
$$ \vec{a}_{cm} = \frac{\sum m_i \vec{a}_i}{\sum m_i} $$\( \vec{a}_{cm} \) is acceleration of a point
$$ \vec{r}_{cm} = \frac{\sum m_i \vec{r}_i}{\sum m_i} $$