Normal-Tangential coordinate systems¶
In some applications its more convinient to express position as a function of velocity along a path,
- Racing a car around a track
- Local path planning
Normal-Tangential coordinate systems¶
- Velocity is always tangent to the path, so choose velocity as one direction
- Normal is the vector from the particle's location to center of curvature.
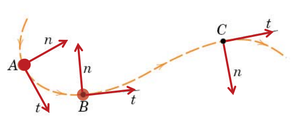
Computing \( \dot{\hat{u}}_t \)¶
Intuitive understanding As \( \hat{u}_t \) is tangential vector along the path, its derivative quantifies how much the path is turning at a given instant.
Mathematical derivation¶
Given distance \( s \) along the path,
$$ \dot{\hat{u}}_t = \frac{d \hat{u}_t}{dt} = \frac{d s}{dt} \frac{d \hat{u}_t}{ds} = v \frac{d \hat{u}_t}{ds} $$Next investigate \( \frac{d \hat{u}_t}{ds} \)¶
\( \frac{d \hat{u}_t}{ds} \) is the rate at which direction of velocity is changing with respect to the path. Denote magnitude of \( \frac{d \hat{u}_t}{ds} \) by curvature \( k \).
$$ k(s) = \left| \frac{d \hat{u}_t}{ds} \right| $$Further,
$$ \hat{u}_t \circ \hat{u}_t = 1$$Therefore,
$$ \frac{d \hat{u}_t}{ds} \circ \hat{u}_t + \hat{u}_t \circ \frac{d \hat{u}_t}{ds} = 0$$ $$2 \frac{d \hat{u}_t}{ds} \circ \hat{u}_t = 0 $$Therefore, \( \frac{d \hat{u}_t}{ds} \) is perpendicular to \( \hat{u}_t \).
Define \( \hat{u}_n \) as (only when \( k(s) \neq 0 \)
$$ \hat{u}_n = \frac{d \hat{u}_t / ds}{ \left| d \hat{u}_t /ds \right| } = \frac{1}{k(s)} \frac{d \hat{u}_t}{ds} $$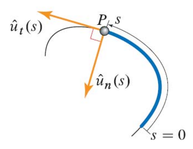
Rewrite, \( k(s) = 1/\rho(s) \)¶
$$ \hat{u}_n = \frac{1}{k(s)} \frac{d \hat{u}_t}{ds} = \rho(s) \frac{d \hat{u}_t}{ds} $$Rearranging
$$\frac{d \hat{u}_t}{ds} = \frac{1}{\rho(s)} \hat{u}_n $$If path is expressed as \( y = f(x) \), then radius of curvature is given by
$$ \rho(x) = \frac{[1 + (dy/dx)^2]^\frac{3}{2}}{\left| d^2 y / dx^2 \right|} $$From before,
$$ \vec{a} = \dot{v} \hat{u}_t + v \dot{\hat{u}}_t $$$$ = \dot{v} \hat{u}_t + \frac{v^2}{\rho} \hat{u}_n $$Where
$$ \rho(x) = \frac{[1 + (dy/dx)^2]^\frac{3}{2}}{\left| d^2 y / dx^2 \right|} $$if \( y = f(x) \).
Relative motion¶
$$ \vec{r}_{B/A} = \vec{r}_{AB} = \vec{r}_{B} - \vec{r}_{A} $$$$ \vec{r}_{B/A} = (x_B - x_A) \hat{i} + (y_B - y_A) \hat{j} $$$$ \vec{v}_{B/A} = \dot{\vec{r}}_{B/A} = (\dot{x}_B - \dot{x}_A) \hat{i} + (\dot{y}_B - \dot{y}_A) \hat{j} $$$$ \vec{a}_{B/A} = \dot{\vec{v}}_{B/A}= \ddot{\vec{r}}_{B/A} = (\dot{v}_{x,B} - \dot{v}_{x,A}) \hat{i} + (\dot{v}_{y,B} - \dot{v}_{y,A}) \hat{j} $$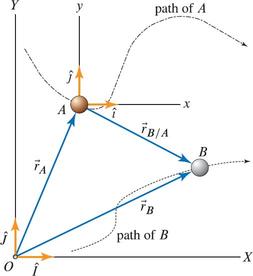
Relative motion¶
$$\vec{r}_{B} = \vec{r}_{B/A} + \vec{r}_{A} $$$$\vec{v}_{B} = \vec{v}_{B/A} + \vec{v}_{A} $$$$\vec{a}_{B} = \vec{a}_{B/A} + \vec{a}_{A} $$Differentiating Geometric constraints: Example 1¶
$$ y_A = L cos(\theta ) $$ $$ x_B = L sin(\theta ) $$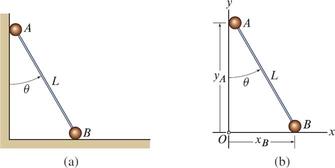
Position¶
$$ y_A = L cos(\theta ) $$ $$ x_B = L sin(\theta ) $$Velocity¶
Taking derivative gives,
$$ v_A = - L \dot{\theta} sin(\theta ) $$ $$ v_B = L \dot{\theta} cos(\theta ) $$Acceleration¶
Taking derivative gives,
$$ v_A = - \frac{d (L \dot{\theta} sin(\theta ) )}{dt} = - L \ddot{\theta} sin(\theta ) - L \dot{\theta}^2 cos(\theta ) $$ $$ v_B = \frac{d (L \dot{\theta} cos(\theta ) )}{dt} = L \ddot{\theta} cos(\theta ) - L \dot{\theta}^2 sin(\theta ) $$Constraint,
$$ L^2 = x_B^2 + y_A^2 $$Taking derivative gives,
$$ 0 = 2 x_B \dot{x}_B + 2 \dot{y}_A y_A $$Differentiating Geometric constraints: Example 2¶
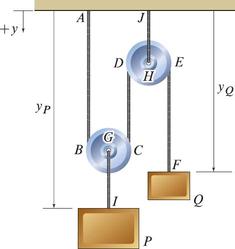
Length of the rope is fixed,
Therefore,
$$L = AB + per(G) + CD + per(H) + EF $$ $$L = (y_P - GI) + per(G) + (y_P-GI-JH) + per(H) + (y_Q - JH) $$