Overview¶
- Time derivative of a Vector
- Polar coordinates
Velocity: Derivative of position vector¶
Consider a vector represented as \( \vec{r} = r \hat{u}_r \) The velocity of the particle is given by \( \dot{\vec{r}} \).
$$ \dot{\vec{r}} = \frac{d \vec{r}}{ dt} = \frac{d r }{ dt} \hat{u}_r+ r \frac{d \hat{u}_r }{ dt} $$A change in the vector \( \vec{r} \) can be due to change in the magnitude \(r \) or \( \hat{u}_r \).
$$ \dot{\vec{r}} = \frac{d \vec{r}}{ dt} = \frac{d r }{ dt} \hat{u}_r+ r \frac{d \hat{u}_r }{ dt} = \dot{r} \hat{u}_r + y \dot{\hat{u}}_r $$Two ways \( \dot{\vec{r}} \) can change,
- change in \( \dot{ r } \), refers to a change in the length of the vector
- change in \( \dot{\hat{u}}_r \), refers to a change in direction of the unit vector
Derivative of a unit vector¶
\( \hat{u}_r \) can be written as,
$$ \hat{u}_r = cos(\theta) \hat{i} + sin(\theta) \hat{j} $$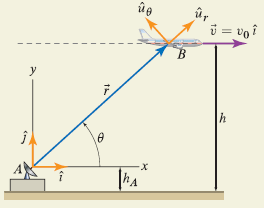
Derivative of \( \hat{u}_r \) is,¶
$$ \dot{\hat{u}}_r = -sin(\theta) \dot{\theta} \hat{i} + cos(\theta) \dot{\theta}\hat{j} $$$$ \dot{\hat{u}}_r = \dot{\theta} \left(-sin(\theta) \hat{i} + cos(\theta) \hat{j} \right)$$
$$ \dot{\hat{u}}_r = \dot{\theta} \left(sin(\theta) \hat{k} \times \hat{j} + cos(\theta) \hat{k} \times \hat{i} \right)$$$$ \dot{\hat{u}}_r = \dot{\theta} \hat{k} \times \left(cos(\theta) \hat{i} + sin(\theta) \hat{j}\right)$$
Derivative of \( \hat{u}_r \) is,¶
$$ \dot{\hat{u}}_r = \dot{\theta} \hat{k} \times \left(cos(\theta) \hat{i} + sin(\theta) \hat{j}\right) = \dot{\theta} \hat{k} \times \hat{u}_r = \vec{\omega } \times \hat{u}_r $$Therefore, derivative of vector \( \vec{r} \) is given by,
$$ \dot{\vec{r}} = \dot{r} \hat{u}_r + r \dot{\hat{u}}_r $$ $$ = \dot{r} \hat{u}_r + r \vec{\omega} \times \hat{u}_r $$Therefore, velocity is given by
$$ \vec{v} = \dot{\vec{r}} = \underbrace{\dot{r} \hat{u}_r}_{change~in~length} + \underbrace{\vec{\omega} \times \vec{r}}_{change~in~direction} $$Acceleration: Second derivative of position vector¶
Given, \( \vec{r} = r \hat{u}_r \) compute acceleration.
From before, velocity is given by,
$$ \vec{v} = \dot{\vec{r}} = \dot{r} \hat{u}_r + \vec{\omega} \times \vec{r} $$Acceleration is derivative of velocity,
$$ \vec{a} = \ddot{\vec{r}} = \dot{\vec{v}} = \ddot{r} \hat{u}_r + \dot{r} \dot{ \hat{u}}_r + \dot{\vec{\omega}} \times \vec{r} +\vec{\omega} \times \dot{ \vec{r}} $$
$$ = \ddot{r} \hat{u}_r + \dot{r} \dot{ \hat{u}}_r + +\dot{\vec{\omega}} \times \vec{r} +\vec{\omega} \times \dot{ \vec{r}} $$
From before,
$$ \dot{ \hat{u}}_r = \vec{\omega} \times \hat{u}_r $$and
$$ \dot{ \vec{r}} = \dot{r} \hat{u}_r + \vec{\omega} \times \vec{r} $$Substituting gives¶
$$ \vec{a} = \ddot{\vec{r}} = \dot{\vec{v}} = \ddot{r} \hat{u}_r + \dot{r} \dot{ \hat{u}}_r + \dot{\vec{\omega}} \times \vec{r} +\vec{\omega} \times \dot{ \vec{r}} $$ $$ = \ddot{r} \hat{u}_r + \dot{r} ( \vec{\omega} \times \hat{u}_r ) + +\dot{\vec{\omega}} \times \vec{r} +\vec{\omega} \times ( \dot{r} \hat{u}_r + \vec{\omega} \times \vec{r} ) $$
$$ = \ddot{r} \hat{u}_r + \dot{r} ( \vec{\omega} \times \hat{u}_r ) +\dot{\vec{\omega}} \times \vec{r} +\vec{\omega} \times ( \dot{r} \hat{u}_r + \vec{\omega} \times \vec{r} ) $$
Rearranging terms gives,
$$ = \ddot{r} \hat{u}_r + 2 \dot{r} ( \vec{\omega} \times \hat{u}_r ) +\dot{\vec{\omega}} \times \vec{r} +\vec{\omega} \times ( \vec{\omega} \times \vec{r} ) $$Position, Velocity and Acceleration of a vector¶
Position
$$ \vec{r} = r \hat{u}_r $$Velocity
$$ \vec{v} = \dot{r} \hat{u}_r + \vec{\omega} \times \vec{r} $$Acceleration
$$ \vec{a} = \underbrace{\ddot{r} \hat{u}_r}_{linear~acceleration} + \underbrace{2 \dot{r} ( \vec{\omega} \times \hat{u}_r ) }_{coriolis} + \underbrace{\vec{\alpha} \times \vec{r}}_{rotational~acceleration} +\underbrace{\vec{\omega} \times ( \vec{\omega} \times \vec{r} ) }_{rotational~acceleration}$$These relations are always true, we will next apply them under specific coordinate frame assumptions¶
Polar coordinates¶
In polar coordinates, we define $ \hat{u}_r $ and $ \hat{u}_\theta $, and simplify previous equations.
Choose coordinate frames such that,
$$ \hat{u}_r, \hat{u}_\theta, ~ and ~ \hat{k} $$are orthogonal, and
$$ \hat{u}_r \times \hat{u}_\theta = \hat{k}$$ $$ \hat{u}_\theta \times \hat{k} = \hat{u}_r $$ $$ \hat{k} \times \hat{u}_r = \hat{u}_\theta $$Under this notation, \( \vec{\omega} = \omega \hat{k} \)
Velocity¶
$$ \vec{v} = \dot{r} \hat{u}_r + \vec{\omega} \times \vec{r} $$ $$ = \dot{r} \hat{u}_r + \omega \hat{k} \times r \hat{u}_r = \dot{r} \hat{u}_r + r \omega \hat{k} \times \hat{u}_r $$ $$ = \dot{r} \hat{u}_r + r \omega \hat{u}_\theta $$Acceleration¶
$$ \vec{a} = \ddot{r} \hat{u}_r + 2 \dot{r} ( \vec{\omega} \times \hat{u}_r ) +\dot{\vec{\omega}} \times \vec{r} +\vec{\omega} \times ( \vec{\omega} \times \vec{r} ) $$$$ \vec{a} = \ddot{r} \hat{u}_r + 2 \dot{r} ( \omega \hat{k} \times \hat{u}_r ) +\alpha \hat{k} \times r \hat{u}_r +\omega \hat{k} \times ( \omega \hat{k} \times r \hat{u}_r ) $$
$$ = \ddot{r} \hat{u}_r + 2 \dot{r} \omega ( \hat{k} \times \hat{u}_r ) +r \alpha \hat{k} \times \hat{u}_r +\omega \hat{k} \times ( \omega \hat{k} \times r \hat{u}_r ) $$$$ = \ddot{r} \hat{u}_r + 2 \dot{r} \omega ( \hat{k} \times \hat{u}_r ) +r \alpha \hat{k} \times \hat{u}_r + r \omega^2 \hat{k} \times ( \hat{k} \times \hat{u}_r ) $$$$ \vec{a} = (\ddot{r} - r \omega^2) \hat{u}_r + (\alpha r + 2 \dot{r} \omega ) \hat{u}_\theta $$