2.1 Kinematics¶
Kinematics describe the motion of a particle or a body without accounting for the forces that may cause the motion.
Kinematics: Position, velocity and acceleration.
Relation between position, velocity and derivative¶
Velocity is derivative of position, and acceleration is derivative of velocity.
Given position vector \( \vec{R} \),
Position vector in cartesian coordinates (x-y).¶
Given a point \( (x_P, y_P) \) the position vector is given by,
$$ \vec{R}_P = x_P \hat{i} + y_P \hat{j} $$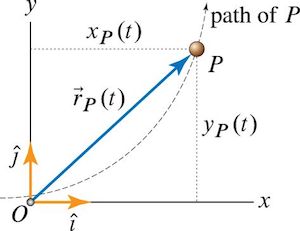
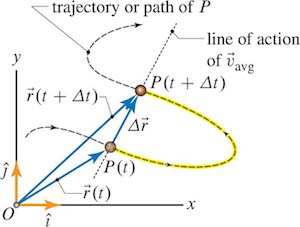
Trajectory and displacement¶
Trajectory is time-history (position vs time) or \( (\vec{r}(t) ) \)
Displacement is difference in position vector between two given time instants. In the figure below, \( \Delta \vec{r} \) is the displacement between times \( t \) and \( t + \Delta t \). $$ \Delta \vec{r} = \vec{r} (t + \Delta t) - \vec{r} (t) $$
Note, displacement of a particle can be zero even if the net distance traveled by the particle is non-zero. For example, a full rotation about a circle brings the particle back to the same position.
Trajectory plotted in the cartesian space is called path (x vs y).
Velocity and speed¶
- Velocity is the rate of change of position.
- Speed is the magnitude of velocity.
- Average velocity is displacement over time. Note, average velocity can be zero, even if the velocity at the intermediate points is not zero.
Average velocity¶
$$ Average ~ Velocity = \frac{Displacement}{time} $$$$Displacement = \Delta \vec{r} = \vec{r} (t + \Delta t) - \vec{r} (t) $$$$ Average ~ Velocity = \frac{ \Delta \vec{r}}{\Delta t} = \frac{\vec{r} (t + \Delta t) - \vec{r} (t) }{\Delta t} $$Velocity vector¶
As \( \Delta t \rightarrow 0 \), the average velocity approaches the true velocity of the particle at a given instant. Therefore, velocity can be computed as,
$$ \vec{v}(t) = \underbrace{Lim}_{\Delta t \rightarrow 0} \frac{ \Delta \vec{r}}{\Delta t} = \frac{ d \vec{r}}{dt} = \dot{\vec{r} } $$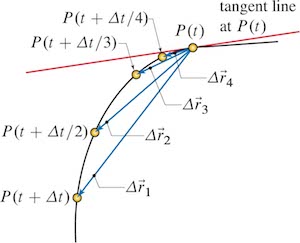
- Velocity vector is always tangent to the path.
Speed along a path¶
Given \( s \) path length along a path, the speed along the path is given by,
$$ v = \frac{ds}{dt} $$Average speed along the track,
$$ v_{avg} = \frac{s_2 - s_1}{t_2 - t_1} $$Acceleration¶
Acceleration is the rate of change of velocity.
$$ \vec{a}(t) = \dot{\vec{v}} = \underbrace{Lim}_{\Delta t \rightarrow 0} \frac{ \vec{v}(t+\Delta t) - \vec{v}(t) }{\Delta t} $$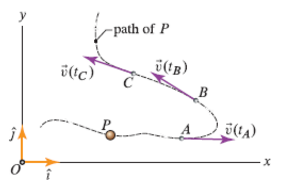
Average and instantaneous acceleration¶
Given the velocity vector \( \vec{v} \), the instantaneous acceleration is given by,
$$ \vec{a} = \frac{d \vec{v}}{dt} $$Average acceleration along the track,
$$ \vec{a}_{avg} = \frac{ \vec{v}_2 - \vec{v}_1}{t_2 - t_1} $$Elementary motions¶
- Linear or rectilinear motion, motion along a straight line
- Rotational motion, rotation of a point around a circle.
Linear or Rectilinear motion¶
For motion in a straight line, we can drop the direction vector and replace it with distance \(s \) from start.
$$ v = \frac{ds}{dt} $$ $$ a = \frac{dv}{dt} = \frac{d^2s}{dt^2} = v \frac{dv}{ds} $$The form of equation to choose depends on the quantify we are interested in and the given expression.
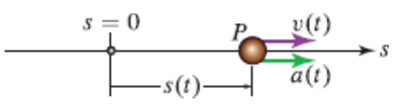
For constant acceleration,
$$v(t) = v(t_0) + a_c (t-t_0) $$ $$s(t) = s(t_0) + v(t_0) (t-t_0) + \frac{1}{2}a_c (t-t_0)^2 $$ $$v(t)^2 = v(t_0)^2 + 2 a_c (s(t)-s(t_0)) $$Circular motion.¶
All relations for rectilinear motion apply directly to the ANGULAR QUANTITIES (angle, angular velocity and angular acceleration).
NOTE: THE RECTILINEAR EQUATIONS DO NOT APPLY TO THE LINEAR KINEMATICS OF A PARTICLE MOVING IN A CIRCLE.
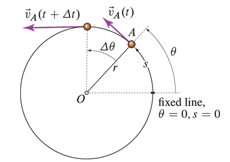
Given angle \( \Theta \), angular velocity is given by,
$$ \omega = \frac{d \Theta}{dt} = \dot{ \Theta} $$ $$ \alpha = \frac{d \omega}{dt} = \frac{d^2 \Theta}{dt^2} = \omega \frac{d \omega}{d \Theta} = \ddot{ \Theta}$$Projectile motion¶
Projectile motion is motion where a particle moves solely under the action of gravity (and sometimes drag). The accelerations, assuming no drag are given by
$$ a_x = 0, ~ a_y = -g = -9.8 ~ m/s^2 $$Given a projectile thrown with a velocity \( v_x(0) \) and \( v_y(0) \), the velocity is given by,
$$ v_x(t) = v_x(0) $$$$ v_y(t) = v_y(0) - g t $$Given a projectile thrown with a velocity \( v_x(0) \) and \( v_y(0) \) from positon \( s_x(0) \) and \( s_y(0) \), distance traveled by the projectile is given by,
$$ s_x(t) = s_x(0) + v_x(0) t $$$$ s_y(t) = s_y(0) + v_y(0) t - \frac{1}{2}g t^2 $$